Figura 1
El ejercicio consiste en obtener las líneas de influencia de todos los apoyos y además la línea de influencia de cortante y de momento flector en el punto H de la viga.
Solución
Primero se procede a dividir la viga en puntos convenientes donde consideremos que es necesario que se apoye la carga unitaria. Este paso puede realizarse a criterio, considerando que mientras más divisiones tenga la viga, existirá más coste computacional.
Entonces, dividiendo la viga de tal forma que los apoyos y el punto H coincidan con nudos tenemos:
La enumeración de los elementos es correlativa:
Y la enumeración de grados de libertad de todos los elementos es la siguiente:
Como las divisiones son equidistantes entre apoyos, existen cinco grupos de elementos de diferentes longitudes, para los cuales deberán armarse las respectivas matrices de rigidez.
La fórmula de cada matriz de rigidez va como sigue:
Entonces, se tienen las siguientes matrices para los cinco tipos de elementos:
Cada una de estas matrices de rigidez viene acompañada de sus respectivos grados de libertad marcados en rojo. Estos grados de libertad ayudan a armar la matriz de rigidez global.
Finalmente ensamblada la matriz de rigidez y armado el sistema de ecuaciones se tiene:
Al lado derecho del sistema de ecuaciones se encuentran los vectores de carga. Por ser este un caso de cargas móviles, se acomodaron lado a lado los vectores de carga para cada caso de carga (cada salto de la carga unitaria al siguiente nudo de izquierda a derecha). El arreglo de vectores de carga mostrado nos sirve para resolver todos los casos de carga de manera simultánea.
Luego se eliminan filas y columnas de la matriz de rigidez de los grados de libertad restringidos (5, 13, 25, 33) pues en estos corresponden a los desplazamientos verticales en los apoyos.
Se resuelve el sistema mediante cualquier método de resolución de sistemas de ecuaciones lineales (por ejemplo Newton Rapson o Jacobi) y se obtienen los desplazamientos en un arreglo matricial para cada estado de carga, de la siguiente manera:
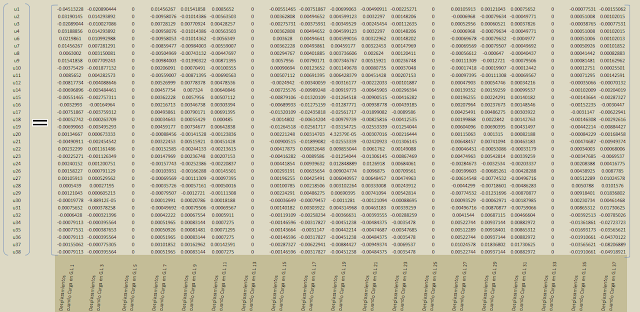
Una vez conocidos los desplazamientos en cada nudo, se pueden reemplazar en el sistema de ecuaciones armado con todos los grados de libertad siguiente:
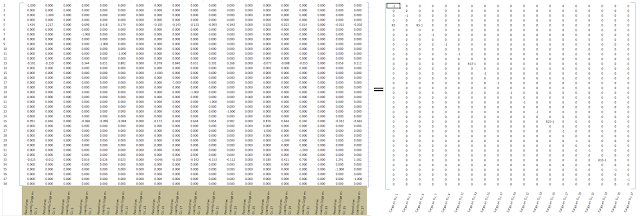
Entonces multiplicando la matriz [K] por {u} se obtienen vectores de las cargas y reacciones ya resueltos.
En los campos donde no exista una Reacción “R” como incógnita, el vector de la izquierda será igual al vector equivalente de la derecha.
En los campos donde exista una reacción “R” incógnita, se deberá despejar esta reacción para conocer el resultado de la reacción final.
Se tiene, así:
En resumen, si por ejemplo se deseara dibujar la Línea de Influencia de reacciones, se puede generar la siguiente tabla resumen:
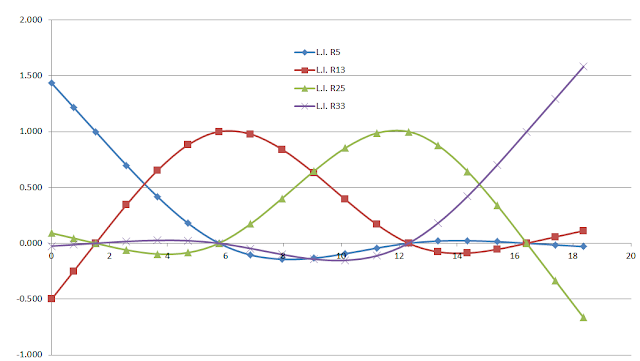
Y graficando todas las líneas de influencia en una sola gráfica, se tiene finalmente:
VOLVER A TABLA DE CONTENIDO
Al lado derecho del sistema de ecuaciones se encuentran los vectores de carga. Por ser este un caso de cargas móviles, se acomodaron lado a lado los vectores de carga para cada caso de carga (cada salto de la carga unitaria al siguiente nudo de izquierda a derecha). El arreglo de vectores de carga mostrado nos sirve para resolver todos los casos de carga de manera simultánea.
Luego se eliminan filas y columnas de la matriz de rigidez de los grados de libertad restringidos (5, 13, 25, 33) pues en estos corresponden a los desplazamientos verticales en los apoyos.
Se resuelve el sistema mediante cualquier método de resolución de sistemas de ecuaciones lineales (por ejemplo Newton Rapson o Jacobi) y se obtienen los desplazamientos en un arreglo matricial para cada estado de carga, de la siguiente manera:
Una vez conocidos los desplazamientos en cada nudo, se pueden reemplazar en el sistema de ecuaciones armado con todos los grados de libertad siguiente:
Entonces multiplicando la matriz [K] por {u} se obtienen vectores de las cargas y reacciones ya resueltos.
En los campos donde no exista una Reacción “R” como incógnita, el vector de la izquierda será igual al vector equivalente de la derecha.
En los campos donde exista una reacción “R” incógnita, se deberá despejar esta reacción para conocer el resultado de la reacción final.
Se tiene, así:
En resumen, si por ejemplo se deseara dibujar la Línea de Influencia de reacciones, se puede generar la siguiente tabla resumen:
Y graficando todas las líneas de influencia en una sola gráfica, se tiene finalmente:
VOLVER A TABLA DE CONTENIDO
Excelente, muchas gracias.
ResponderEliminarcjimenez7m@gmail.com
ResponderEliminarExcelente trabajo
ResponderEliminar